Pengukuran Sudut : Derajat dan Radian

Nama : Aulia Maheswari

Kelas : X MIPA 3 

Absen : 6

Matematika Wajib, SMAN 63 Jakarta 

Pengukuran Sudut : Derajat dan Radian


Konsep dasar pengukuran sudut adalah membagi satu lingkaran penuh dengan satuan tertentu. Ada tiga pengukuran yang masih banyak digunakan sampai saat ini yaitu : derajat, grad, dan radian. Tetapi yang paling umum dipakai adalah derajat dan radian.


Untuk menemukan hubungan radian dan derajat, kita dapat menggunakan konsep perbandingan sudut pusat dan panjang busur. 



sudut pusat = 1 rad
panjang busur = r
keliling = 2πr
 

Secara umum, untuk menentukan hasil pengukuran besaran suatu sudut dinyatakan dalam derajat (1^{o}) dan radian (rad).

Ukuran Sudut dalam Derajat

Ukuran suatu sudut pusat untuk satu putaran penuh yaitu 360^{o}. Dari definisi di atas dapat ditarik kesimpulan bahwa satu derajat (1^{o}) merupakan besarnya sudut yang dibentuk oleh \frac{1}{360} kali putaran.


Contoh 

Perhatikan gambar posisi parabola berikut. Berapa derajat perbedaan antara sudut arah sinar datang dengan sudut elevasi parabola? (dihitung dari 0o)


Jawab:

 

Besar sudut sinar datang dihitung dari 0o adalah 50o, sedangkan sudut elevasi parabola menunjukkan angka 27o. Berarti perbedaan antara sudut sinar datang dengan sudut elevasi adalah 23o.

Ukuran Sudut dalam Radian

Ukuran suatu sudut pusat yang besarnya sama yang panjang  busurnya sama dengan jari-jari lingkaran.

Jika panjang busur tidak sama dengan r, maka cara menentukan besar sudut tersebut dalam satuan radian dapat dihitung dengan menggunakan perbandingan:

Jika panjang busur tidak sama dengan r, maka cara menentukan besar sudut tersebut dalam satuan radian dapat dihitung dengan menggunakan perbandingan:

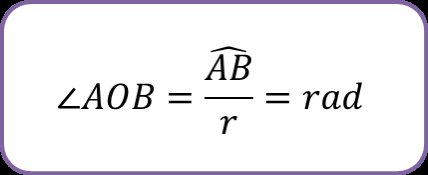
Sudut pusat suatu putaran penuh adalah 2π radian.


Tabel Panjang Busur Lingkaran dengan Sudut Radian

Contoh : 

Pada lingkaran dengan jari-jari 30 inci, panjang busur yang dipotong oleh sudut pusat sebesar  radian adalah ….

Jawab:

s = r θ

s = 30 inci ×  = 10 inci

 

 

Pada lingkaran dengan jari-jari 10 inci, panjang busur yang dipotong oleh sudut pusat sebesar 50o adalah ….

Jawab:

s = r θ

(Ingat: 1 radian =  dan 1°=  )

Sehingga 50° =  radian

s = 10 inci ×  =  inci

 

Hubungan antara Derajat dan Radian

Dari uraian di atas, maka dapat disimpulkan:

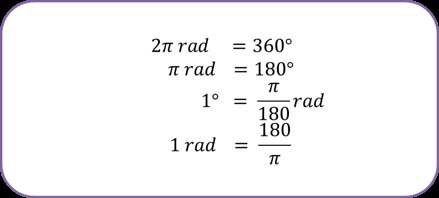
Contoh:

1. Nyatakan sudut-sudut berikut dalam ukuran radian!

  1. 37^{o}

  2. 45^{o}

Jawaban:

  1. 37^{o} = 37^{o} \times \frac{\Pi }{180^{o}} rad = \frac{37}{180}\Pi rad

  2. 45^{o} = 45^{o} \times \frac{\Pi }{180^{o}} rad = \frac{45}{180}\Pi rad = \frac{\Pi }{4}rad

 

2. Nyatakan sudut-suut berikut dalam ukuran radian!

  1. \frac{1}{3}\Pi \, \: rad

  2. \frac{4}{5}\Pi \, \: rad

Jawaban:

  1. \frac{1}{3}\Pi \, \: rad = \frac{1}{3}\Pi \times \frac{180^{o}}{\Pi } =60^{o}

  2. \frac{4}{5}\Pi \, \: rad = \frac{4}{5}\Pi \times \frac{180^{o}}{\Pi } =144^{o}

3. Nyatakan dalam bentuk derajat dan radian!

  1. 2 putaran

  2. \frac{3}{4} putaran

Jawaban:

  1. 2\times 360^{o}=720^{o} \; atau \; 720^{o} = 720^{o}\times \left ( \frac{\Pi }{180^{o}} \right ) rad = 4\Pi \: rad

  2. \frac{3}{4}\times 360^{o}=270^{o} \; atau \; 270^{o} = 270^{o}\times \left ( \frac{\Pi }{180^{o}} \right ) rad = \frac{3}{2}\Pi \: rad

Catatan:

Sudut istimewa yang sering digunakan


 Daftar Pustaka : 

Komentar

Posting Komentar

Postingan populer dari blog ini

SOAL KONTEKSTUAL BERKAITAN PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU, SUDUT ELEVASI DAN SUDUT DEPRESI

Gambar
Nama : Aulia Maheswari  Kelas  : X MIPA 3  Absen : 6  Matematika wajib, SMAN 63 Jakarta SOAL KONTEKSTUAL BERKAITAN PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU, SUDUT ELEVASI DAN SUDUT DEPRESI Sudut Elevasi adalah sudut yang terbentuk oleh garis horizontal dengan mata pengamat dengan arah pandang ke atas . Sudut Depresi adalah sudut yang terbentuk oleh garis horizontal dengan mata pengamat dengan arah pandang ke bawah. Masalah Kontekstual mengenai Sudut Elevasi dan Sudut Depresi 1. Sebuah pohon berjarak 130 meter dari seorang pengamat dengan tinggi mata pengamat dari tanah adalah 168 cm. Apabila sudut elevasi yang terbentuk adalah 60° dari mata pengamat ke pucuk pohon, maka tinggi pohon tercebut adalah …. Jawab: Dik : Jarak pengamat ke pohon: 130 meter         Tinggi pengamat: 168 cm = 1,68 meter          Sudut Elevasi 60° Dit : Tinggi pohon ?  Penyelesaian : Pertama. Buatlah ilustrasinya Kedua. Buatlah pemisal...
Baca selengkapnya

LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Gambar
Nama : Aulia Maheswari  Kelas : X MIPA 3  Absen : 6  Matematika Wajib, SMAN 63 Jakarta  LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN Pada dasarnya bangun datar segi-n beraturan terbentuk dari lingkaran yang dibagi-bagi menjadi beberapa bagian yang sama besar (berbentuk segitiga sama kaki). Sehingga untuk menghitung luas dan keliling bangun datar segi-n kita akan melibatkan sudut pusat dan jari-jarinya. Sudut pusatnya adalah sudut pada segitiga dengan besarnya adalah yang ditunjukkan oleh tanda sudut warna 360°/ n yang ditunjukkan oleh tanda sudut warna merah. Sementara sisi dari bangun datar segi-n ditunjukkan oleh huruf x. Rumus Luas Segi - n Beraturan Segi-n beraturan yaitu bangun datar atau bentuk dimensi 2 yang terdiri dari garis-garis bersambungan membentuk bangun tertutup dengan  sisi yang sama panjang dan  sudut yang sama besar.   Jumlah besar sudut dalam segi-n ber...
Baca selengkapnya