SISTEM PERTIDAKSAMAAN KUADRAT-LINEAR DAN BEBERAPA CONTOH SOALNYA

Nama : Aulia Maheswari

Kelas : X MIPA3

Absen : 6

Matematika Wajib, SMAN 63 Jakarta

SISTEM PERTIDAKSAMAAN KUADRAT-LINEAR

Apa itu SPKDV ?

Sistem pertidaksamaan kuadrat dua variabel adalah sistem pertidaksamaan yang terbentuk dari dua atau lebih pertidaksamaan kuadrat dua variabel dengan variabel- variabel yang sama.

Pertidaksamaan adalah bentuk/kalimat matematis, memuat tanda lebih dari “ > “, kurang dari “ < “, lebih dari atau sama dengan “ ≥ “, dan kurang dari atau sama dengan “ ≤ “.

Bentuk dari pertidaksamaan linear

♦ Bentuk Pertidaksamaan

ax + by > c
ax + by < b
ax + by ≥ b
ak + by ≤ b

♦ Contoh kalimat dari pertidaksamaan

3x + 5y > 12
6x – 2y < 8
13x + 15y ≥ 24
15x + 8y ≤ 16

Penyelesaian Pertidaksamaan Linear Dua Variabel

Langkah – langkah penyelesaian pertidaksamaan linear dua variabel:

Ubah tanda pertidaksamaan menjadi tanda sama dengan (=).
Cari nilai dari titik saat dan sebaliknya.
Gambar grafik garis yang menghubungkan kedua titik.
Arsir daerah yang bersesuaian dengan tanda pertidaksamaan.

Contoh Penjelasan Soal

1. 3x + 4y ≤12

Jawab:

Sebagai contoh disini kita mengambil titik daerah lainnya yaitu (0,0) agar mempermudah anda dalam pengerjaannya. Lalu dengan titik (0,0) tersebut akan diperoleh bilangan seperti ini:

3x + 4y ≤12

= 3 (0) + 4 (0) ≤ 12

= 0 + 0 ≤ 12

= 0 ≤ 12 ( Nol kurang dari sama dengan dua belas)

Sehingga diperoleh 0≤12 benar, yang berarti sangat memenuhi sebagai daerah penyelesaian (DP).

Mencari nilai x dan y dari tabel

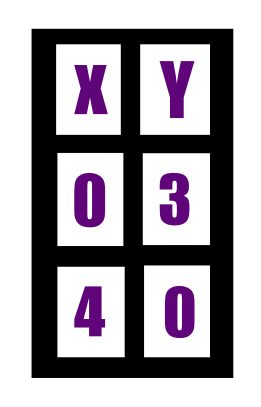
Mencari nilai x dan y

dari gambar diatas dapat diketahui bahwa untuk nilai x = (4,0) dan untuk nilai y = (0,3).

Jadi daerah penyelesaiannya yaitu daerah yang masuk dalam titik (0,0). yakni daerah yang di arsir pada gambar berikut ini.

Sehingga, himpunan penyelesaian pertidaksamaan dari soal ini adalah {x | x < −3, x ∈ R}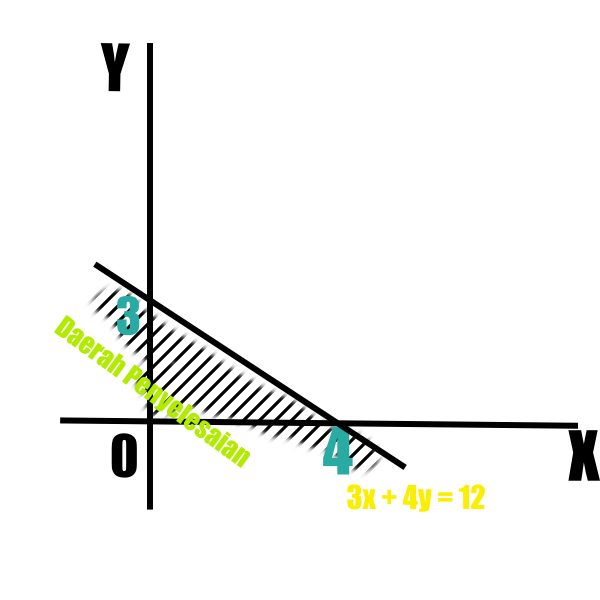

2. Tentukan himpunan penyelesaian pertidaksamaan linear di bawah ini:

4– 3x ≥ 4x + 18

Solusi =

4 – 3x ≥ 4x + 18

−4x – 3x ≥ −4 + 1

−7x ≥ 14

x ≤ −2

Sehingga, himpunan penyelesaian pertidaksamaan dari soal nomor 1 yaitu {x | x ≤ −2, x ∈ R}

3. Tentukan himpunan penyelesaian pertidaksamaan linear di bawah ini:

8x + 1 < x – 20

Solusi =

8x – x < −20 – 1

7x < −21

x < −3

Sehingga, himpunan penyelesaian pertidaksamaan dari soal ini adalah {x | x < −3, x ∈ R}

4. Sebuah gerobak hanya bisa membawa beban kurang dari 20 kg. Satu keranjang apel memiliki berat sebesar 4 kg dan satu keranjang mangga memiliki berat sebesar 1 kg. Berapa keranjang apel dan mangga yang dapat dibawa oleh 1 buah gerobak jika banyaknya keranjang yang dibawa oleh gerobak minimum harus 10 keranjang?

Jawab:

Jika diubah ke dalam bentuk model matematika, soal cerita di atas akan menjadi:

4x + y < 20
x + y >= 10

Langkah 1: mencari nilai dari titik saat dan sebaliknya dari tiap pertidaksamaan

Terlebih dahulu pertidaksamaan di atas kita ubah menjadi bentuk persamaan, yaitu:

4x + y = 20 dan x + y >= 10

Pertidaksamaan 1:

Saat y = 0 , maka 4x = 20 sehingga x = 5 .

Saat x = 0 , maka y = 20 .

Sehingga diperoleh titik – titik $\left ( 5, 0 \right ) dan \left ( 0, 20 \right )$ .

Pertidaksamaan 2:

Saat y = 0 , maka x = 10 .

Saat x = 0 , maka y = 10 .

Sehingga diperoleh titik – titik $\left ( 10, 0 \right ) dan \left ( 0, 10 \right )$ .

Langkah 2: Menggambar grafik garis yang menghubungkan kedua titik

Pertidaksamaan 1:

Berikut ini merupakan grafik garis yang menghubungkan titik $\left ( 5, 0 \right ) dan \left ( 0, 20 \right )$ :

Pertidaksamaan 2:

Berikut ini merupakan grafik garis yang menghubungkan titik $\left ( 10, 0 \right ) dan \left ( 0, 10 \right )$ :

Langkah 3: mengarsir daerah penyelesaian dari SPtLDV

Daerah di bawah garis adalah tanda untuk kurang dari () dan daerah di atas garis adalah untuk tanda lebih dari (). Daerah dari SPtLDV 4x + y < 20 dan x + y >= 10 adalah:

Salah satu titik penyelesaian di atas adalah x = 1 dan y = 12 . Jadi, gerobak tersebut bisa membawa 1 keranjang apel dan 12 keranjang mangga dengan total berat $(4 \ times 1) + (1 \times 12) = 4 + 12 = 16$ kg (kurang dari 20 kg) dan total karung 13 (lebih dari 10 karung).

5. contoh soal dibawah ini

6. Gambarlah daerah penyelesaian pertidaksamaan kuadrat y > x² – 8x + 12
Jawab =

(1) Tititk potong dengan sumbu-X syarat y = 0
x² – 8x + 12 = 0
(x – 6)(x – 2) = 0
x = 6 dan x = 2 Titik potongnya (2, 0) dan (6, 0)

(2) Tititk potong dengan sumbu-Y syarat x = 0
y = x² – 8x + 12
y = (0)² – 8(0) + 12
y = 12 Titik potongnya (0, 12)
Menentukan titik minimum fungsi y = x² – 8x + 12

Gambar daerah penyelesaiannya (Daerah yang diarsir adalah daerah penyelesaian)

7. Gambarlah daerah penyelesaian dari sistem pertidaksamaan 2x + 3y ≥ 12 dan y ≤ –x² + 2x + 8 dalam tata koordinat Cartesius!
Jawab =
Pertama akan digambar daerah penyelesaian 2x + 3y ≥ 12

Selanjutnya digambar juga daerah penyelesaian y ≤ –x² + 2x + 8, dengan langkah langkah :
Menentukan tititk potong dengan sumbu-X syarat y = 0
–x² + 2x + 8 = 0
x² – 2x – 8 = 0
(x – 4)(x + 2) = 0
x = –2 dan x = 4 . Titik potongnya (–2 0) dan (4, 0)

Menentukan tititk potong dengan sumbu-Y syarat x = 0
y = –x² + 2x + 8
y = –(0)² + 2(0) + 8
y = 8 . Titik potongnya (0, 8)

Menentukan titik maksimum fungsi y = –x² + 2x + 8

Menggambar daerah penyelesaiannya (Daerah yang diarsir adalah daerah penyelesaian)

Irisan dari kedua daerah penyelesaian tersebut merupakan penyelesaian dari sistem pertidaksamaan 2x + 3y ≥ 12 dan y ≤ –x² + 2x + 8
Gambar daerahnya adalah sebagai berikut:

Daftar Pustaka =

https://www.kelaspintar.id/blog/tips-pintar/himpunan-penyelesaian-pertidaksamaan-pengertian-dan-cara-menyelesaikannya-8378/
https://mardinata.com/pertidaksamaan-kuadrat-dua-variabel/
https://edura.id/blog/matematika/sistem-pertidaksamaan-linear-dua-variabel/amp/
https://www.materimatematika.com/2017/11/sistem-pertidaksamaan-linier-dan-kuadrat.html?m=1

Cari Blog Ini

Aulia Maheswari