SISTEM PERTIDAKSAMAAN KUADRAT-KUADRAT & CONTOH SOALNYA

Nama : Aulia Maheswari 

Kelas : X MIPA 3 

Absen : 6 

Matematika Wajib, SMAN 63 Jakarta 

 SISTEM PERTIDAKSAMAAN KUADRAT-KUADRAT

 

Sistem pertidaksamaan kuadrat dua variabel terdiri dari dua pertidaksamaan kuadrat. Salah satu metoda yang paling populer dalam menyelesaikannya adalah dengan metoda grafik. 

Bentuk umum sistem pertidaksamaan dua variabel kuadrat-kuadrat , yaitu : 

 

a, b, c bilangan real dan a ≠ 0.

Langkah-Langkah Penyelesaian

Langkah 1

Tentukanlah pembuat nol dengan cara merubah tanda pertidaksamaan hingga menjadi “sama dengan”. Akar-akar persamaan kuadrat yang didapat yaitu pembuat nol.

x2 + x – 6 = 0 ,difaktorkan
menjadi (x +3)(x-2) = 0

Pembuat nol dari persamaan tersebut bisa dicari dengan memakai cara ini..

Pertama gunakan :
x + 3 = 0
x = -3

Kedua kita gunakan :
x – 2 = 0
x = 2

Maka, pembuat nolnya sudah didapat yaitu -3 dan 2.

Langkah 2
Gambarlah pembuat nol pada garis bilangan, Lalu tentukan tanda masing-masing interval dengan cara mensubstitusi sembarang bilangan yang ada pada tiap interval ke persamaan pada ruas kiri. Tulis (+) adai hasil substitusi adalah bernilai positif dan tulis (−) jika hasil substitusi adalah bernilai negatif.

Catatan :
Tanda untuk tiap interval yaitu slalu berselang-seling (+)(−)(+) atau (−)(+)(−), kecuali jika akar-akar yang didapat sama (kembar)

Tips :
Jika akar-akar yang didapat berbeda, cukup cari tanda pada satu interval saja, sisanya tinggal ditulis berselang-seling mengikuti pola diatas. Dahulukan interval yang memuat angka nol agar perhitungan lebih mudah (jika nol bukan merupakan pembuat nol).

Langkah 3
Tentukanlah daerah penyelesaian atau arsiran.
Untuk pertidaksamaan “>” atau “≥”, daerah penyelesaian yang berada pada interval bertanda positif (+).
Untuk pertidaksamaan “<” atau “≤”, daerah pernyelesaian yang berada pada interval bertanda negatif (−).

Langkah 4
Tulis sebuah himpunan penyelesaian, yaitu interval yang memuat daerah penyelesaian.

Himpunan penyelesaian ada pada ujung-ujung interval

 

CONTOH SOAL 

1. Gambarlah kedua pertidaksamaan kuadrat berikut ini dalam satu sistem koordinat Cartesius, kemudian tentukan daerah penyelesaiannya
y > x² – 9
y ≤ –x² + 6x – 8

Jawab = 

(1) Tititk potong dengan sumbu-X syarat y = 0
      x² – 9 = 0
     (x + 3)(x – 3) = 0
      x = –3 dan x = 3
Titik potongnya (–3, 0) dan (3, 0)

(2) Tititk potong dengan sumbu-Y syarat x = 0
      y = x² – 9
      y = (0)² – 9
      y = –9
Titik potongnya (0, –9)

(3) Menentukan titik minimum fungsi y = x² – 9

(4) Gambar daerah penyelesaiannya
(Daerah yang diarsir adalah daerah penyelesaian)

2. Gambar daerah penyelesaian pertidaksamaan y ≤ –x² + 6x – 8

Jawab = 

(1) Tititk potong dengan sumbu-X syarat y = 0
      –x² + 6x – 8 = 0
        x² – 6x + 8 = 0
     (x – 4)(x – 2) = 0
      x = 4 dan x = 2
Titik potongnya (4, 0) dan (2, 0)

(2) Tititk potong dengan sumbu-Y syarat x = 0
      y = –x² + 6x – 8
     y = –(0)² + 6(0) – 8
     y = –8
Titik potongnya (0, –8)

(3) Menentukan titik maksimum fungsi y = –x² + 6x – 8



(4) Gambar daerah penyelesaiannya
(Daerah yang diarsir adalah daerah penyelesaian)


Daerah penyelesaian kedua pertidaksamaan itu adalah irisan dua daerah penyelesaian masing-masing pertidaksamaannya, yakni:

3. Tentukan HP dari −x² − 3x + 4 > 0

Jawab = 

Pembuat nol
−x² − 3x + 4 = 0
x² + 3x − 4 = 0
(x+4) (x−1) = 0
x = −4 atau x = 1

Untuk interval −4 < x < 1, ambil x = 0
−x² − 3x + 4 = −(0)² − 3(0) + 4 = 4 (+)

Karena pertidaksamaan bertanda “>” , Jadi, daerah penyelesaian ada pada interval yang bertanda (+).
∴ HP = {−4 < x < 1}

4. Tentukanlah HP dari x² − 2x − 3 ≥ 0

Jawab =

Pembuat nol
x² − 2x − 3 = 0
(x+1) (x−3) = 0
x = −1 atau x = 3

Untuk interval −1 < x < 3, ambil x = 0
x² − 2x − 3 = (0)² − 2(0) − 3 = −3 (−)

Karena pertidaksamaan bertanda “≥” , Jadi, daerah penyelesaian ada pada interval yang bertanda (+).
∴ HP = {x ≤ −1 atau x ≥ 3}

5.  x(3x + 1) < (x + 1)² − 1

Jawab = 

Terlebih dulu ubah dalam bentuk umum pertidaksamaan kuadrat yaitu:
x(3x + 1) < (x + 1)² − 1
⇔ 3x² + x < x² + 2x + 1 − 1
⇔ 2x² − x < 0

Pembuat nol :
2x² − x = 0
x ( 2x − 1 ) = 0
x = 0 atau x = 1/2

Untuk interval x > 1/2 maka ambil x = 1
2x² − x = 2(1)² − 1 = 1 (+)

Sebab pertidaksamaan bertanda “<” , Jadi, daerah penyelesaian ada pada interval yang bertanda (−).
∴ HP = {0 < x < 1/2}

6. Dio akan melemparkan bola dan menginginkan ketinggian bolanya paling tidak mencapai 8t-t². Indra akan melempar bola 2 detik setelah Dio dan menginginkan ketinggian bolanya paling tidak mencapai 10t-t² (t dalam detik). Pada detik keberapa bola Dio dan bola Indra akan berada pada ketinggian yang sama? Berapa ketinggiannya?

Jawab =

h₁ = Ketinggian bola Dio

h₂ = Ketinggian bola Indra

Menentukan pertidaksamaan untuk ketinggian masing-asing bola.

h₁ ≤ 8t-t2

Bola indra dilempar 2 detik setelah bola Dio,maka:

h₂ ≤ 10(t-2) - (t-2)2↔ h₂ ≤ 10t-20 - (t2 – 4t + 4)

h₂ ≤ 10t-20 - t2 + 4t – 4

h₂ ≤ - t2 + 14t – 24

Ketinggian tidak boleh nol, maka h₁ ≥ 0 dan h₂ ≥ 0

Sistem pertidaksamaan yang menyatakan ketinggian dari kedua bola pada waktu (t) yang bersamaan adalah:

Dengan h₁ ≥ 0 dan h₂ ≥ 0

Langkah selanjutnya adalah menggambar grafik h₁ = -t2 + 8t, kemudian menggambar grafik

h₂ = -t2 + 14t – 24

1. Menggambar grafik h₁ = -t2 + 8t

1. h1 = -t2 + 8t merupakan parabola yang mempunyai nilai a = -1 ,b = 8 dan c = 0. a = -1 , maka parabola terbuka kebawah.
2. Titik potong dengan sumbu t.
   h = 0↔-t2 + 8t = 0
   ↔t (-t + 8) = 0
   ↔t = 0 atau t = 8.
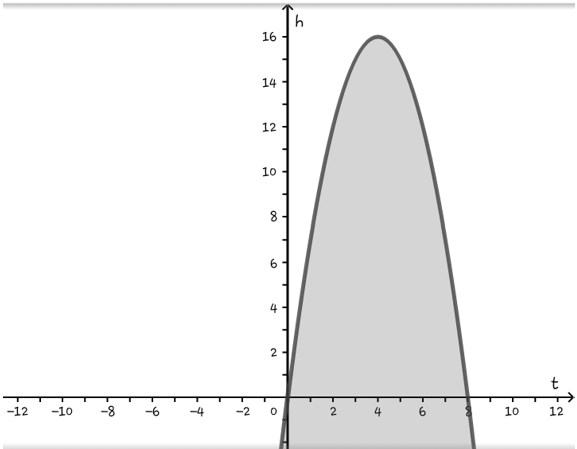
   Jadi , titik potong grafik h1 = -t2 + 8 dengan sumu t adalah (0,0) dan (8,0).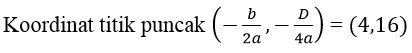
3. 
4. Uji titik untuk menentukan daerah pertidaksamaan. Ambil sembarang titik dibawah kurva, misalkan (1,0). Subtitusikan pada pertidaksamaan h₁ ≤ -t2 + 8t diperoleh 0 < 7. Jadi daerah pertidaksamaan h₁ ≤ -t2 + 8t berada dibawah kurva h₁ = -t2 + 8t. Karena h₁ ≥ 0 , maka diperoleh daerah penyelesaian seperti diatas.
5. 

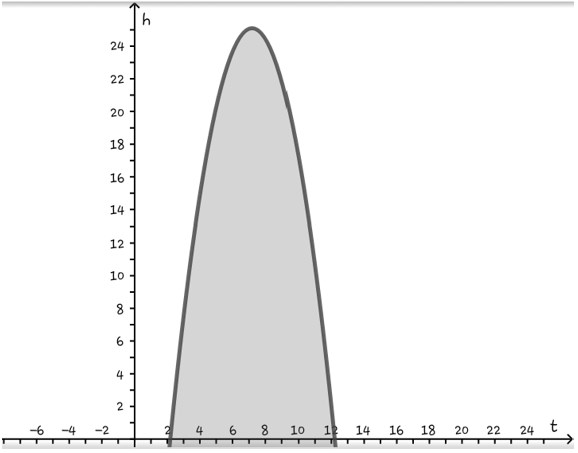
2. Menggambar grafik h2 = -t2 + 14t – 24.
   h2 = -t2 + 14t – 24 merupakan parabola yang mempunyai nilai a = -1 ,b = 14 dan c = -24.
   a = -1, maka parabola terbuka ke bawah.
   Titik potong dengan sumbu t.
   h = 0↔- t2 + 14t – 24 = 0
   ↔ t2 - 14t + 24 = 0
   ↔(t – 2) (t – 12)= 0
   ↔t = 2 atau t = 12.

Jadi, titik potong dengan sumbu t adalah (2,0) dan (12,0).

Koordinat titik puncak (-b/2a,-D/4a) = (7,25)

Uji titik untuk menentukan daerah pertidaksamaan.

Ambil sembarang titik dibawah kurva, misalkan (5,0). Subtitusikan pada pertidaksamaan h₂ ≤ -t2 + 14t – 24 diperoleh 0 < 21. Jadi, daerah pertidaksamaan h₂ ≤ -t2 + 14t – 24 berada dibawah kurva h₂ = -t2 + 14t – 24. Karena h₂ ≥ 0, maka diperoleh daerah penyelesaian seperti dibawah.

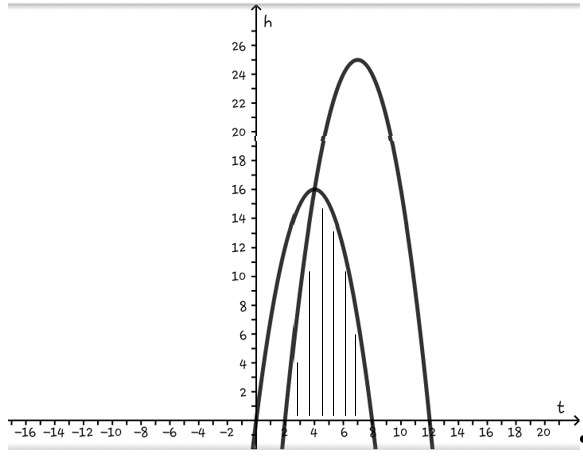
Langkah selanjutnya adalah menggabungkan kedua kuadrat grafik dalam satu sistem koordinat cartesius seperti gambar dibawah.

Diperoleh daerah himpunan penyelesaian dari sistem pertidaksamaan tersebut yang merupakan irisan dari masing-masing daerah himpunan penyelesaian pertidaksamaan kuadrat yang membentuknya.

Daftar Pustaka 

• https://mas-alahrom.my.id/pelajaran/mapel/mtk/sistem-pertidaksamaan-kuadrat-dua-variabel
• https://www.materimatematika.com/2017/11/sistem-pertidaksamaan-kuadrat-dan.html 
• https://www.sambimatika.my.id/2021/08/sistem-pertidaksamaan-dua-variabel-kuadrat-kuadrat.html?m=1
• https://rumus.co.id/pertidaksamaan-kuadrat/