SOAL FUNGSI: KUADRAT, RASIONAL, IRASIONAL

Nama : Aulia Maheswari

Kelas : X MIPA 3

Absen : 6

Matematika Wajib, SMAN 63 Jakarta 

SOAL FUNGSI: KUADRAT, RASIONAL, IRASIONAL

# Fungsi Kuadrat # 

Fungsi kuadrat adalah relasi kuadrat yang digunakan untuk menghubungkan antara daerah asal dan daerah hasil. Bentuk umum fungsi kuadrat ditulis dengan

y = ax² + bx + c dengan a ≠ 0.

Keterangan:
Nilai a adalah koefisien dari x²
Nilai b adalah koefisien dari x
Nilai c adalah konstanta

Contoh Soal Bentuk Umum Fungsi Kuadrat

1. f(x) = 4x² + 3x + 8. Hitunglah nilai a + 2b + 3c!

Jawaban:

Diketahui nilai a = 4, b = 3, c = 8
= a + 2b + 3c
= 4 + 2(3) + 3(8)
= 4 + 6 + 24
= 34

2. f(x) = 3x² - 2x + 5 memiliki bentuk sesuai dengan bentuk f(x) = ax² + bx + c. Hitunglah nilai 2a + 3b + 4c!

Jawaban:

= Diketahui nilai a = 3, b = -2, c = 5
= 2a + 3b + 4c
= 2(3) + 3(-2) + (4 x 5)
= 6 - 6 + 20
= 20

3. Diketahui fungsi f(x) = x² + 4x + 5. Hitunglah bayangangan untuk nilai x = 3

Jawaban:
= f(x) = x² + 4x + 5
= f(3) = 3² + 4(3) + 5
= f(3) = 9 + 12 + 5
= f(3) = 26 

Grafik Fungsi Kuadrat 

Dikarenakan berupa fungsi, maka fungsi kuadrat dapat digambarkan grafiknya. Bentuk grafik kuadrat ini menyerupai parabola.
Nilai a pada fungsi y = ax² + bx + c akan memengaruhi bentuk grafik.

Jika nilai a positif, grafiknya akan terbuka ke atas. Sebaliknya, jika nilai a negatif, grafiknya akan terbuka ke bawah. Kemudian, jika nilai a semakin besar maka grafiknya menjadi lebih "kurus".

Nilai b pada grafik y = ax² + bx + c menunjukkan letak koordinat titik puncak dan sumbu simetri. Jika a > 0, grafik y = ax² + bx + c memiliki titik puncak minimum. Jika a < 0, grafik y = ax² + bx + c memiliki titik puncak maksimum.
Nilai c pada grafik y = ax² + bx + c menunjukkan titik perpotongan grafik fungsi kuadrat tersebut dengan sumbu-y, yakni pada koordinat (0, c).

cara yang digunakan untuk menentukan sumbu simetri dan titik puncak/maksimum.

Diketahui fungsi kuadrat adalah f(x) = ax² + bx + c
Menentukan sumbu simetri adalah x = -(b/2a)
Menentukan nilai titik puncak adalah y0 = -(b²- 4ac/4a) atau y0= -(D/4a) 

Contoh soal:

1. Diketahui fungsi kuadrat y = 2x2 + 4x - 6. Tentukan sumbu simetrinya!

Jawaban:
= x = -(b/2a)
= x = -(4/2x2)
= x = -(4/4) = -1

Jadi, sumbu simetrinya adalah x = -1

2. Diketahui fungsi kuadrat y = 3x2 + 6x + 5. Tentukan titik puncaknya!

Jawaban:Tentukan sumbu simetri terlebih dahulu

= x = -(b/2a)
= x = -(6/2x3)
= x = -(6/6) = -1

Jadi, sumbu simetrinya adalah x = -1

Tentukan titik puncak
= y0 = -(b²- 4ac/4a)
= y0 = -(6²- 4x3x5/4x3)
= y0 = -(36-60/12)
= y0 = -(-24/12)
= y0 = 2

Jadi, titik puncaknya adalah (-1, 2)

3. Suatu fungsi kuadrat f(x) = ax² - 4x + c mempunyai titik puncak di (1, 4). Tentukan nilai f(x)!

Jawaban:

Pertama, substitusikan koordinat x pada titik puncak ke dalam rumus sumbu simetri untuk mendapatkan nilai a
= 1 = -(b/2a)
= 1 = -(-4/2a)
= 1 = 2/a
= a = 2

Kemudian, substitusikan nilai a dan koordinat puncak (1, 4) ke fungsi kuadrat f(x) = ax² - 6x + c untuk mendapatkan nilai c
= 1 = (2x1²) - (6x1) + c
= 1 = 2 - 6 + c
= 1 = -5 + c
= 1 + 5 = c
= 6 = c

Terakhir, untuk menemukan nilai f(x), substitusikan nilai a dan c ke dalam f(x) = ax² - 6x + c

= f(x) = ax² - 6x + c
= f(x) = 2(x²) - 6(x) + 3
= f(x) = 2x² - 6x + 3

Jadi, nilai f(x) = 2x² - 6x + 3
 

4. Suatu fungsi kuadrat f(x) = ax² - 8x + c mempunyai titik puncak di (2, 3). Tentukan nilai f(3)!

Jawaban:
Pertama, substitusikan koordinat x pada titik puncak ke dalam rumus sumbu simetri untuk mendapatkan nilai a
= 2 = -(b/2a)
= 2 = -(-8/2a)
= 2 = 4/a
= a = 2
Kemudian, substitusikan nilai a dan koordinat puncak (2, 3) ke fungsi kuadrat f(x) = ax² - 8x + c untuk mendapatkan nilai c
= 2 = (2x2²) - (8x2) + c
= 2 = 8 - 16 + c
= 2 = -8 + c
= 10 = c
= 10 = c
Terakhir, untuk menemukan nilai f(3), substitusikan x = 3, nilai a dan c ke dalam f(x) = ax² - 8x + c
= f(x) = ax² - 8x + c
= f(3) = (2x3²) - (8x3) + 10
= f(3) = 18 - 24 + 10
= f(3) = 4
Jadi, nilai f(3) adalah 4

5. Tentukan nilai maksimum dari fungsi y = x2 – x – 6.

Pembahasan

Nilai maksimum dari suatu fungsi kuadrat adalah

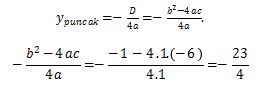
Contoh Soal Titik Puncak

Jadi, ypuncak = – 23/4

6. Jika titik puncak dari grafik y = x2 + px + q adalah (2, 3), tentukan nilai p + q.

Pembahasan

Dengan menggunakan rumus titik puncak koordinat x, maka:

–b/2a = 2

–p/2×1 = 2

p = 2 × 2 × (-1)

p = -4

Dengan mensubstitusikan titik puncak (2, 3) dan nilai p ke persamaan y = x2 + px + q diperoleh:

3 = 22 + -4(2) + q

3 = 4 – 8 + q

q = 1

Maka

p + q = -4 + 1 = -3

Jadi, nilai p + q adalah -3.

7. Jika fungsi y = ax2 + 8x + (a+2) mempunyai sumbu simetri x = 2, carilah koordinat titik puncaknya.

Pembahasan

Sumbu simetri berada di x titik puncak, sehingga:

–b/2a = 2

–8/2a = 2

a = -2

Dengan mensubstitusikan nilai a ke fungsi y, diperoleh:

y = ax2 + 8x + (a+2)

y = -2x2 + 8x

Maka kita dapat menentukan koordinat titik puncak y, yaitu

-(b2 – 4ac) / 4a = -(82 – 4(-2)(0)) / 4(-2)

-(b2 – 4ac) / 4a = – 64 / -8

-(b2 – 4ac) / 4a = 8

Jadi, koordinat titik puncaknya adalah (2, 8).

# Fungsi Rasional dan Irasional # 

Pertidaksamaan irasional dan rasional matematika ipa kelas 10. Titik potong pada sumbu xtitik potong pada sumbu x  . Contoh soal fungsi rasional kuadrat. Dengan dan adalah polinom polinom dan hx.

erikut ini adalah cara yang digunakan untuk menentukan sumbu simetri dan titik puncak/maksimum.

Diketahui fungsi kuadrat adalah f(x) = ax² + bx + c
Menentukan sumbu simetri adalah x = -(b/2a)
Menentukan nilai titik puncak adalah y0 = -(b²- 4ac/4a) atau y0= -(D/4a)

Baca artikel detikedu, "Contoh Soal Fungsi Kuadrat Lengkap dengan Pembahasan" selengkapnya https://www.detik.com/edu/detikpedia/d-5737885/contoh-soal-fungsi-kuadrat-lengkap-dengan-pembahasan.

Download Apps Detikcom Sekarang https://apps.detik.com/de
Fungsi kuadrat adalah relasi kuadrat yang digunakan untuk menghubungkan antara daerah asal dan daerah hasil. Bentuk umum fungsi kuadrat ditulis dengan

y = ax² + bx + c dengan a ≠ 0.


Keterangan:
Nilai a adalah koefisien dari x²
Nilai b adalah koefisien dari x
Nilai c adalah konstanta

Baca juga:
Kumpulan Soal Pembagian Kelas 2 SD untuk Pelajaran Matematika

Contoh Soal Bentuk Umum Fungsi Kuadrat

1. f(x) = 4x² + 3x + 8. Hitunglah nilai a + 2b + 3c!

Jawaban:

Diketahui nilai a = 4, b = 3, c = 8
= a + 2b + 3c
= 4 + 2(3) + 3(8)
= 4 + 6 + 24
= 34

2. f(x) = 3x² - 2x + 5 memiliki bentuk sesuai dengan bentuk f(x) = ax² + bx + c. Hitunglah nilai 2a + 3b + 4c!

Jawaban:

= Diketahui nilai a = 3, b = -2, c = 5
= 2a + 3b + 4c
= 2(3) + 3(-2) + (4 x 5)
= 6 - 6 + 20
= 20

3. Diketahui fungsi f(x) = x² + 4x + 5. Hitunglah bayangangan untuk nilai x = 3

Jawaban:
= f(x) = x² + 4x + 5
= f(3) = 3² + 4(3) + 5
= f(3) = 9 + 12 + 5
= f(3) = 26

Baca artikel detikedu, "Contoh Soal Fungsi Kuadrat Lengkap dengan Pembahasan" selengkapnya https://www.detik.com/edu/detikpedia/d-5737885/contoh-soal-fungsi-kuadrat-lengkap-dengan-pembahasan.

Download Apps Detikcom Sekarang https://apps.detik.com/detik/
1. f(x) = 4x² + 3x + 8. Hitunglah nilai a + 2b + 3c!

Jawaban:

Diketahui nilai a = 4, b = 3, c = 8
= a + 2b + 3c
= 4 + 2(3) + 3(8)
= 4 + 6 + 24
= 34

2. f(x) = 3x² - 2x + 5 memiliki bentuk sesuai dengan bentuk f(x) = ax² + bx + c. Hitunglah nilai 2a + 3b + 4c!

Jawaban:

= Diketahui nilai a = 3, b = -2, c = 5
= 2a + 3b + 4c
= 2(3) + 3(-2) + (4 x 5)
= 6 - 6 + 20
= 20

3. Diketahui fungsi f(x) = x² + 4x + 5. Hitunglah bayangangan untuk nilai x = 3

Jawaban:
= f(x) = x² + 4x + 5
= f(3) = 3² + 4(3) + 5
= f(3) = 9 + 12 + 5
= f(3) = 26

Baca artikel detikedu, "Contoh Soal Fungsi Kuadrat Lengkap dengan Pembahasan" selengkapnya https://www.detik.com/edu/detikpedia/d-5737885/contoh-soal-fungsi-kuadrat-lengkap-dengan-pembahasan.

Download Apps Detikcom Sekarang https://apps.detik.com/detik/

Komentar

Posting Komentar

Postingan populer dari blog ini

SOAL KONTEKSTUAL BERKAITAN PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU, SUDUT ELEVASI DAN SUDUT DEPRESI

Gambar
Nama : Aulia Maheswari  Kelas  : X MIPA 3  Absen : 6  Matematika wajib, SMAN 63 Jakarta SOAL KONTEKSTUAL BERKAITAN PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU, SUDUT ELEVASI DAN SUDUT DEPRESI Sudut Elevasi adalah sudut yang terbentuk oleh garis horizontal dengan mata pengamat dengan arah pandang ke atas . Sudut Depresi adalah sudut yang terbentuk oleh garis horizontal dengan mata pengamat dengan arah pandang ke bawah. Masalah Kontekstual mengenai Sudut Elevasi dan Sudut Depresi 1. Sebuah pohon berjarak 130 meter dari seorang pengamat dengan tinggi mata pengamat dari tanah adalah 168 cm. Apabila sudut elevasi yang terbentuk adalah 60° dari mata pengamat ke pucuk pohon, maka tinggi pohon tercebut adalah …. Jawab: Dik : Jarak pengamat ke pohon: 130 meter         Tinggi pengamat: 168 cm = 1,68 meter          Sudut Elevasi 60° Dit : Tinggi pohon ?  Penyelesaian : Pertama. Buatlah ilustrasinya Kedua. Buatlah pemisal...
Baca selengkapnya

Pengukuran Sudut : Derajat dan Radian

Gambar
Nama : Aulia Maheswari Kelas : X MIPA 3  Absen : 6 Matematika Wajib, SMAN 63 Jakarta  Pengukuran Sudut : Derajat dan Radian Konsep dasar pengukuran sudut adalah membagi satu lingkaran penuh dengan satuan tertentu. Ada tiga pengukuran yang masih banyak digunakan sampai saat ini yaitu : derajat, grad, dan radian. Tetapi yang paling umum dipakai adalah derajat dan radian. Untuk menemukan hubungan radian dan derajat, kita dapat menggunakan konsep perbandingan sudut pusat dan panjang busur.  sudut pusat = 1 rad panjang busur = r keliling = 2πr   Secara umum, untuk menentukan hasil pengukuran besaran suatu sudut dinyatakan dalam derajat ( ) dan radian ( rad ). Ukuran Sudut dalam Derajat Ukuran suatu sudut pusat untuk satu putaran penuh yaitu  . Dari definisi di atas dapat ditarik kesimpulan bahwa satu derajat ( ) merupakan besarnya sudut yang dibentuk oleh  kali putaran. Contoh  Perhatikan gambar posisi parabola berikut. Berapa derajat perbeda...
Baca selengkapnya

LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN

Gambar
Nama : Aulia Maheswari  Kelas : X MIPA 3  Absen : 6  Matematika Wajib, SMAN 63 Jakarta  LUAS SEGI-n BERATURAN, JARI-JARI LINGKARAN LUAR DAN LINGKARAN DALAM SEGITIGA, GARIS SINGGUNG PERSEKUTUAN LUAR/DALAM LINGKARAN Pada dasarnya bangun datar segi-n beraturan terbentuk dari lingkaran yang dibagi-bagi menjadi beberapa bagian yang sama besar (berbentuk segitiga sama kaki). Sehingga untuk menghitung luas dan keliling bangun datar segi-n kita akan melibatkan sudut pusat dan jari-jarinya. Sudut pusatnya adalah sudut pada segitiga dengan besarnya adalah yang ditunjukkan oleh tanda sudut warna 360°/ n yang ditunjukkan oleh tanda sudut warna merah. Sementara sisi dari bangun datar segi-n ditunjukkan oleh huruf x. Rumus Luas Segi - n Beraturan Segi-n beraturan yaitu bangun datar atau bentuk dimensi 2 yang terdiri dari garis-garis bersambungan membentuk bangun tertutup dengan  sisi yang sama panjang dan  sudut yang sama besar.   Jumlah besar sudut dalam segi-n ber...
Baca selengkapnya